Codebox Software

I wrote some software that uses machine learning to play the game Connect 4, you can try it out online.

For this project my objective was not to produce the strongest possible Connect 4 player. For a relatively simple game such as Connect 4 it is possible to quickly calculate the optimal move (and therefore play perfectly) using search-based methods which rely on exhaustive game simulation, checking many possible board positions and winning by brute-force calculation.

Instead I wanted to experiment with a different approach based on Deep Reinforcement Learning, similar to the one used by the Alpha Zero system developed by Google's DeepMind. This type of system does not rely on planning dozens of steps ahead, or simulating gameplay to check the possible outcomes of each move. Rather it learns from experience, in much the same way that humans do, eventually being able to recognise what 'good' and 'bad' board positions look like, even positions it has never seen before.

This requires a lot of work up-front - such systems must be 'trained' sometimes for long periods of time, before they can achieve good results. However, once this training is complete relatively few calculations are required while actually playing a game. Such systems can also perform well at very complex tasks, where trying to explore every possible action at each step is impractical.

Since this work was based on some of the ideas from DeepMind's Alpha Zero project, I had little choice but to call my system 'Connect Zero' (a name which puny humans will soon learn to fear).

Monte-Carlo Tree Search

In order to assess the strength of Connect Zero I first developed a separate piece of software for it to play against. This software uses an algorithm called Monte-Carlo Tree Search (MCTS) which has the advantage that it can easily be tuned to play at different levels of ability. MCTS works by trying out each of the possible moves that could be played from the current position in lots of simulated games against itself. It starts off picking moves at random, but over time concentrates on those moves that seem to give it a better chance of winning. The longer the algorithm is allowed to run, the better moves it will find.

When referring to a player using this algorithm I use the abbreviation 'MCTS-' followed by the number of simulated games that are being used. For example a 'MCTS-1000' player simulates 1000 games before deciding on what move to play.

Neural Networks

Connect Zero decides how to play by looking at the board positions that would result from each available move, evaluating each of them using a Neural Network, and then playing the best one. The technical term for the role that the Neural Network is playing in this system is a Value Function Approximator - when you show a board position to the network it gives you back a numeric score indicating how much value it assigns to that position (i.e. how good it thinks it is).

Self-Play Reinforcement Learning

The Neural Network was trained using 'self-play', which is exactly what it sounds like: two opponents play many games against each other, both selecting their moves based on the scores returned by the network. As such, the network is learning to play the game completely from scratch with no outside help. The games that it plays against other types of opponent, such as MCTS, are used only to check its progress and the results of those games are not used for training.

At the end of each training game the network receives some feedback about how well its recommended moves worked. The scores for the board positions recommended to the losing player are all reduced slightly, and those recommended to the winning player are increased.

The scores for board positions occurring towards the end of the game (i.e. closer to the eventual victory or loss) are adjusted by larger amounts than the scores for earlier positions, in other words they are apportioned a larger amount of the credit or blame for what happened.

Neural Network Design

Neural Networks come in many shapes and sizes. Selecting the best design is not an exact science, and generally involves some trial and error. I tested 4 designs for this project before picking the one that performed the best.

All 4 designs were types of 'Convolutional Neural Network' (CNN). This type of network is most commonly used for image processing because it excels at learning from 2-dimensional data. Given the grid-like structure of a Connect 4 board they seemed like a natural choice for this project as well.

Neural Networks are composed of multiple 'layers' of different types. Deciding on the type, size, and arrangement of these layers is probably the most important design decision that must be made when building one. CNNs are usually constructed with one or more Convolutional Layers followed by one or more Fully Connected Layers.

Convolutional Layers

A Convolutional Layer takes a 2-dimensional grid of numbers as its input. In order to process a Connect 4 board, the board must be converted into a grid of numbers, for example by using '0' to represent an empty position, and '+1' and '-1' to represent positions occupied by the red and yellow pieces:

A convolutional layer processes its input using a 'filter' which can be thought of as a small square box. The filter is moved over the input from left to right and top to bottom covering the entire input field.

At each position the filter generates a set of numbers that in some way represent the input values at that position. The numbers produced by the filters at each position form a new grid of values, which then become the input for the next layer in the network.

Fully-Connected Layers

A Fully Connected Layer comprises an array of 'neurons', each of which takes all the input values for that layer and produces a single output value. The combined output values of all the neurons in the layer become the input for the next layer in the network.

Designing a Neural Network for Connect 4

The 4 network designs that I tried are shown below. In these diagrams the convolutional layers are represented by the square grids, and the fully connected layers by the columns with circles in them. The size of the square grids indicates the filter sizes used for convolving over the grids. The numbers indicate the size of each layer.

I thought that the 4x4 filters might perform well, since the networks need to be good at finding lines of 4 pieces. However sometimes more layers with smaller filters perform better than fewer layers with large filters, so I tried both approaches. To test the designs I played each one against 3 different algorithmic opponents of different strengths.

First I played each network against a very weak player that just selected moves at random. This is effectively what a new, untrained neural network does, so I expected the games to be evenly matched at first, with the networks taking the lead as they learned. This is more or less what I saw, although I was surprised how quickly the networks were able to start winning:

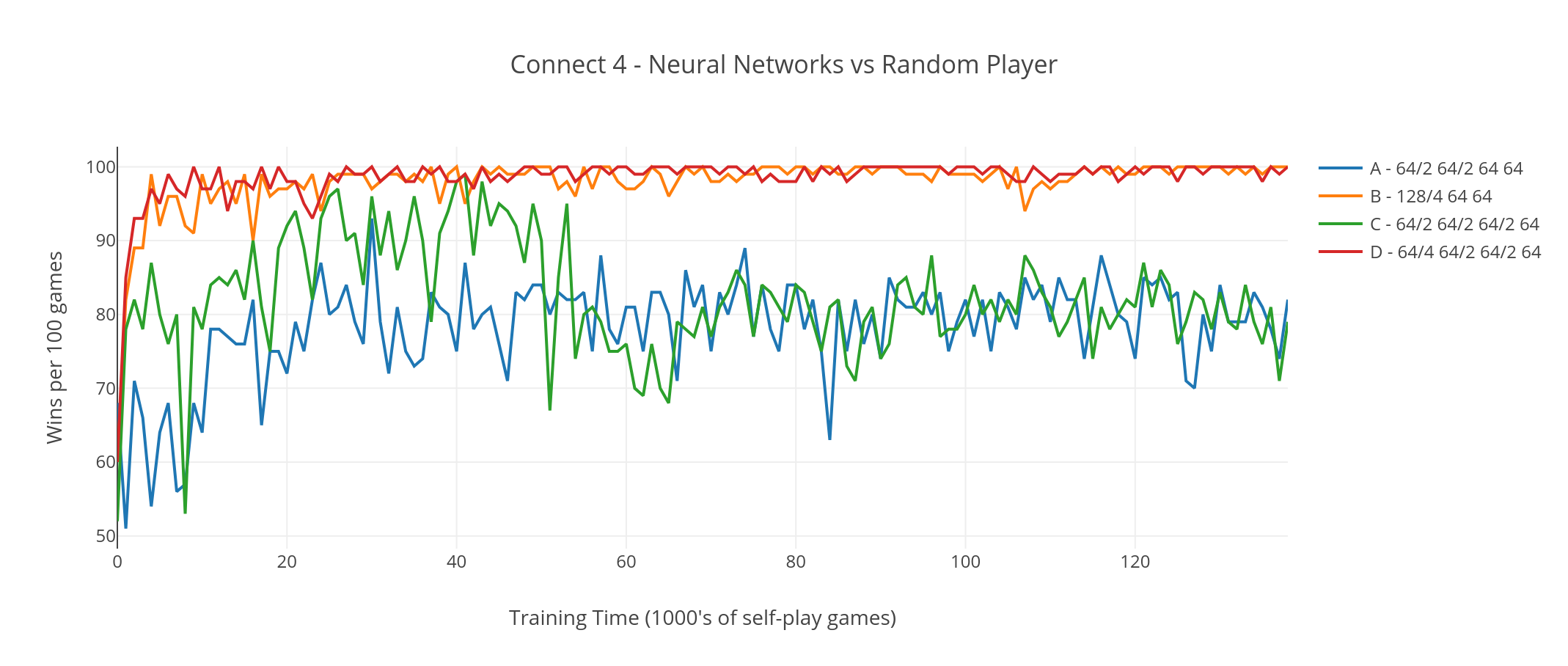
Networks B and D (the two that had 4x4 filters) were winning more-or-less all their games after 10,000 self-play games, but Networks A and C could not consistently win more than 80% of the time.

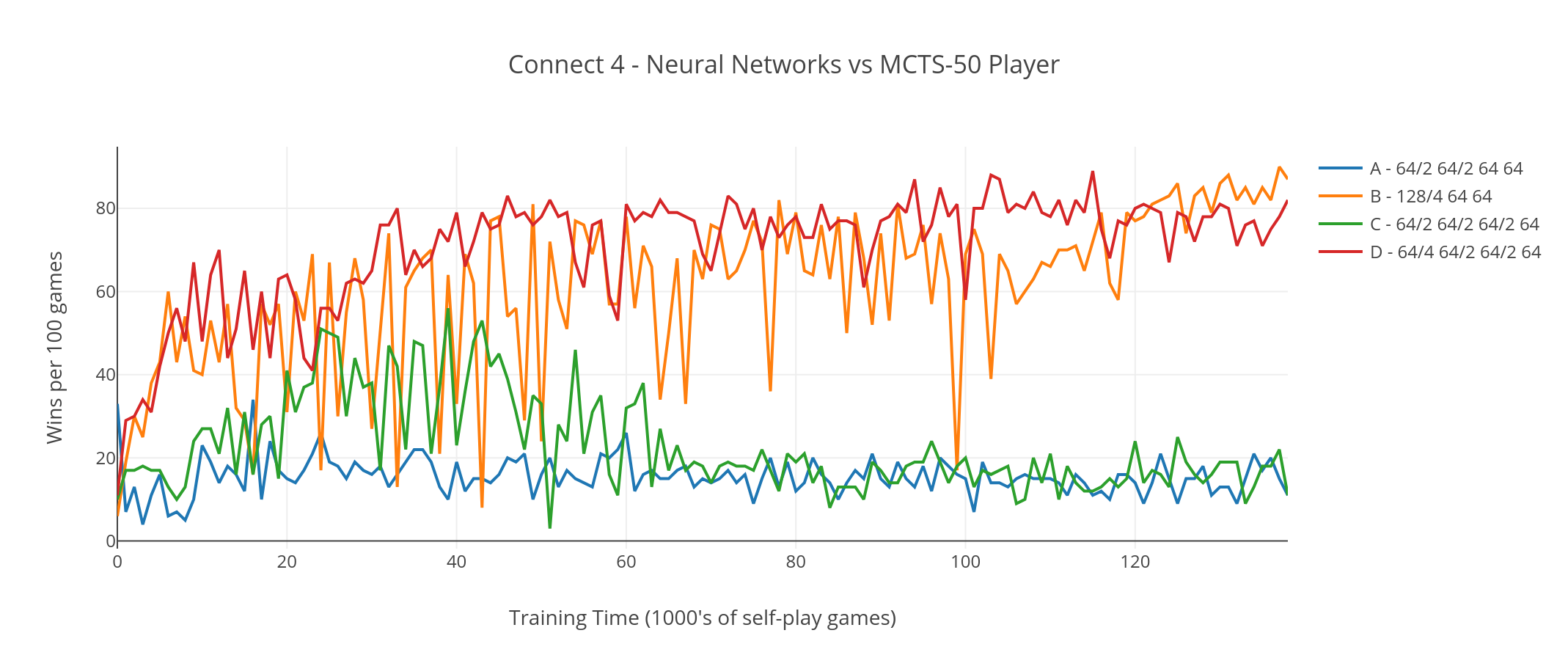
Next I played the networks against a stronger opponent using MCTS-50 (Monte-Carlo Tree Search that runs 50 exploratory games for each move it plays). At this level MCTS is still a very weak player, but is significantly better than just picking moves at random. The results were similar to last time, with the 2 networks that used 4x4 filters doing much better than the 2 that didn't, achieving roughly an 80% win rate by the end of the training time.

Finally I repeated the tournament against a MCTS-250 player. Here Networks A and C hardly managed to win any games at all:

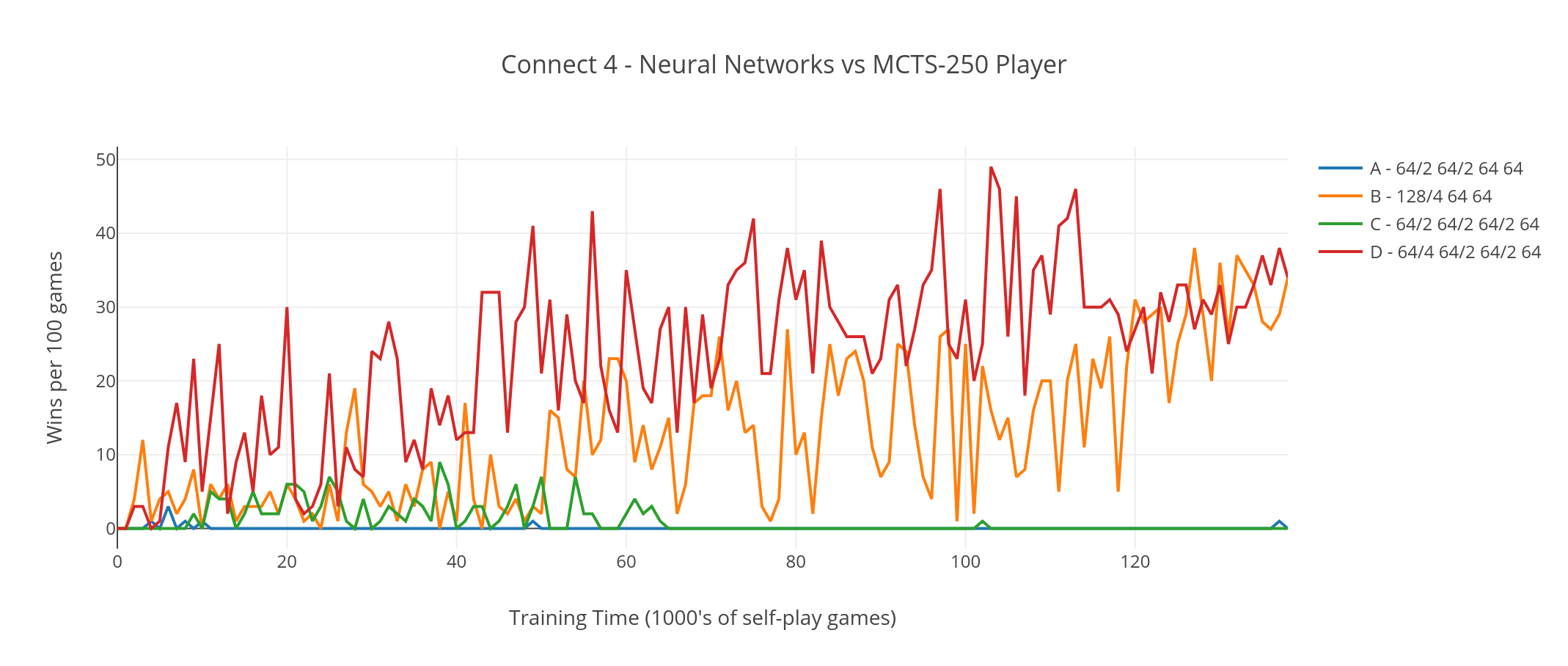
Networks B and D were obviously the stronger players, and after some additional testing I decided that Network B was the most promising candidate, and used this design going forward.

Next I ran a prolonged self-play training session, allowing the network to train for over 6 million games, testing it against a MCTS-1000 player every 10,000 games. The results were interesting - the network improved steadily for the first 5 million games, but then peaked at a level where it was winning around 60% of its games. After that point it actually started getting worse, and I stopped training once performance had dropped to around 40%.

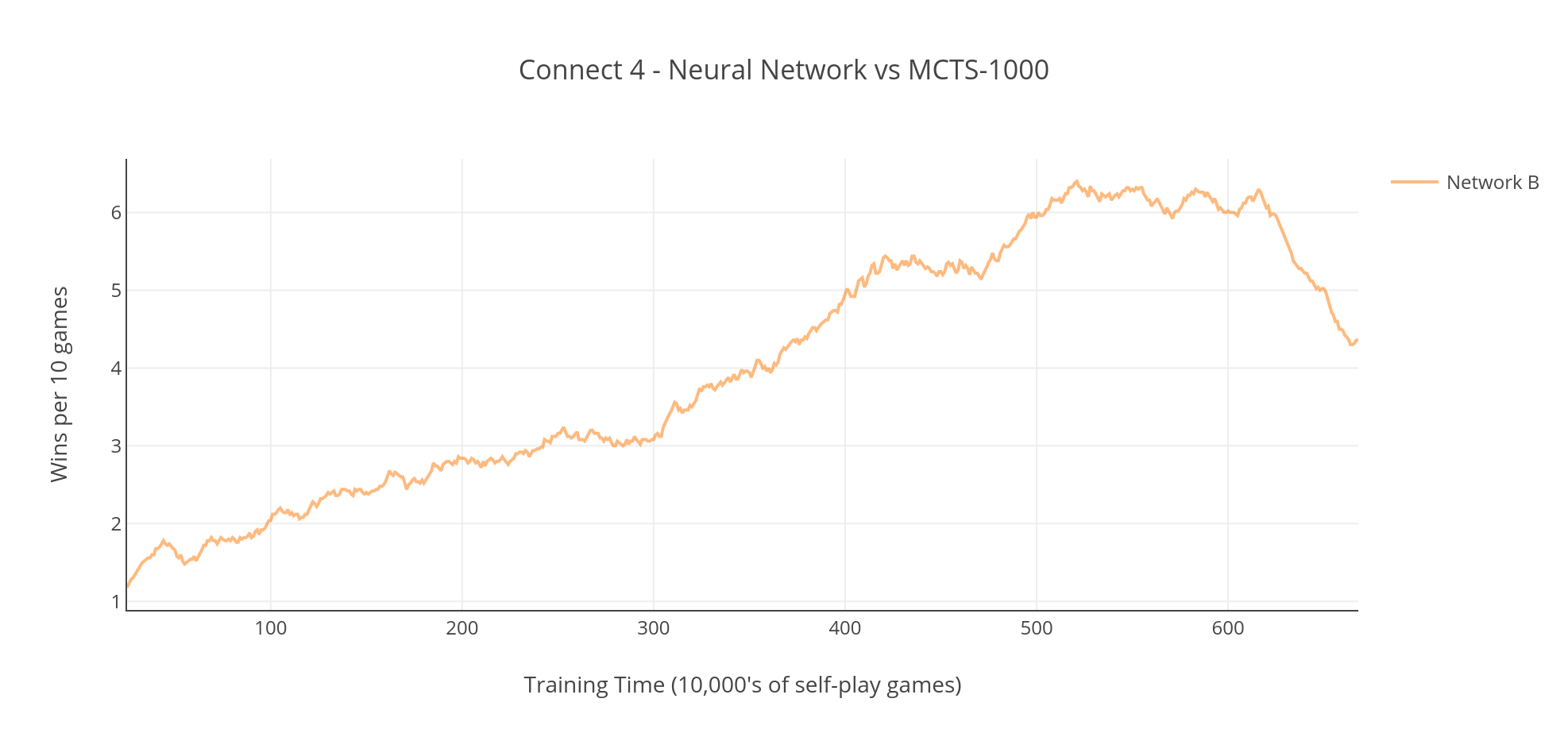
I suspect that the drop in performance was caused by over-fitting. Over-fitting is a common problem in machine learning systems, it occurs when a model adapts to perform well on the data that is being used to train it, but fails to generalise and performs poorly on data that it was not exposed to during training. In this case I think the strategies which the network learned during the later part of its self-play training were giving good results in its training games, but were not effective when tested against an opponent that played in a different style.

To address this problem I created a group of 3 independent networks (each with the same Network B architecture) and trained them against each other. I hoped that because the networks were each learning independently, the differences in their playing styles would force them to develop more general strategies that would be effective against a variety of different opponents. This approach seemed to work - not only did the performance of all 3 networks improve more quickly than before, but there was no sign of the performance degrading over time. Performance seemed to peak at around 68% which was slightly higher than the 64% attained previously.

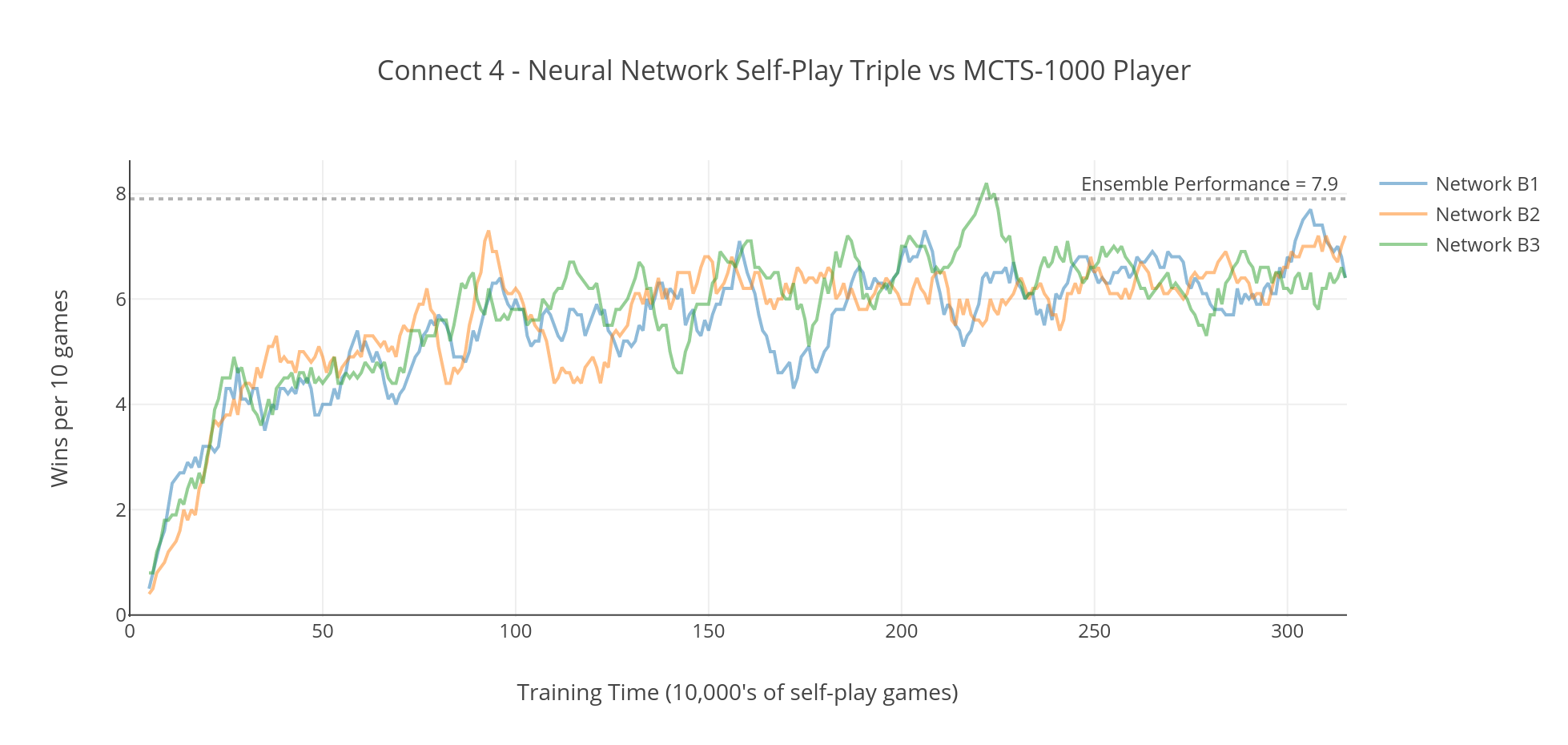
Finally, I combined the 3 networks into an ensemble, using the combined scores returned by all 3 networks to evaluate each board position. This gave a further boost in performance up to 79%.

Up to this point, the Neural Network players' strategy had been simply to select the move that immediately yielded the best looking position. The algorithm never looked beyond the next move, and made no attempt to simulate what an opponent might do next, or to look a few moves ahead and see what the longer term outcomes for each move might be. Although this myopic approach meant that the players could select their moves very quickly, it seemed likely that their play would improve if they looked ahead and considered what would happen further in the future.

I used the MiniMax algorithm to allow Connect Zero to simulate the next few moves of the game, and to take the outcome into account when deciding on its next move.

The MiniMax algorithm assumes that an opponent will always play the best move that is available to them, and then it selects the move which will give the opponent the least opportunity to do damage. In other words, it minimizes the player's loss in the worst-case (maximum loss) scenario.

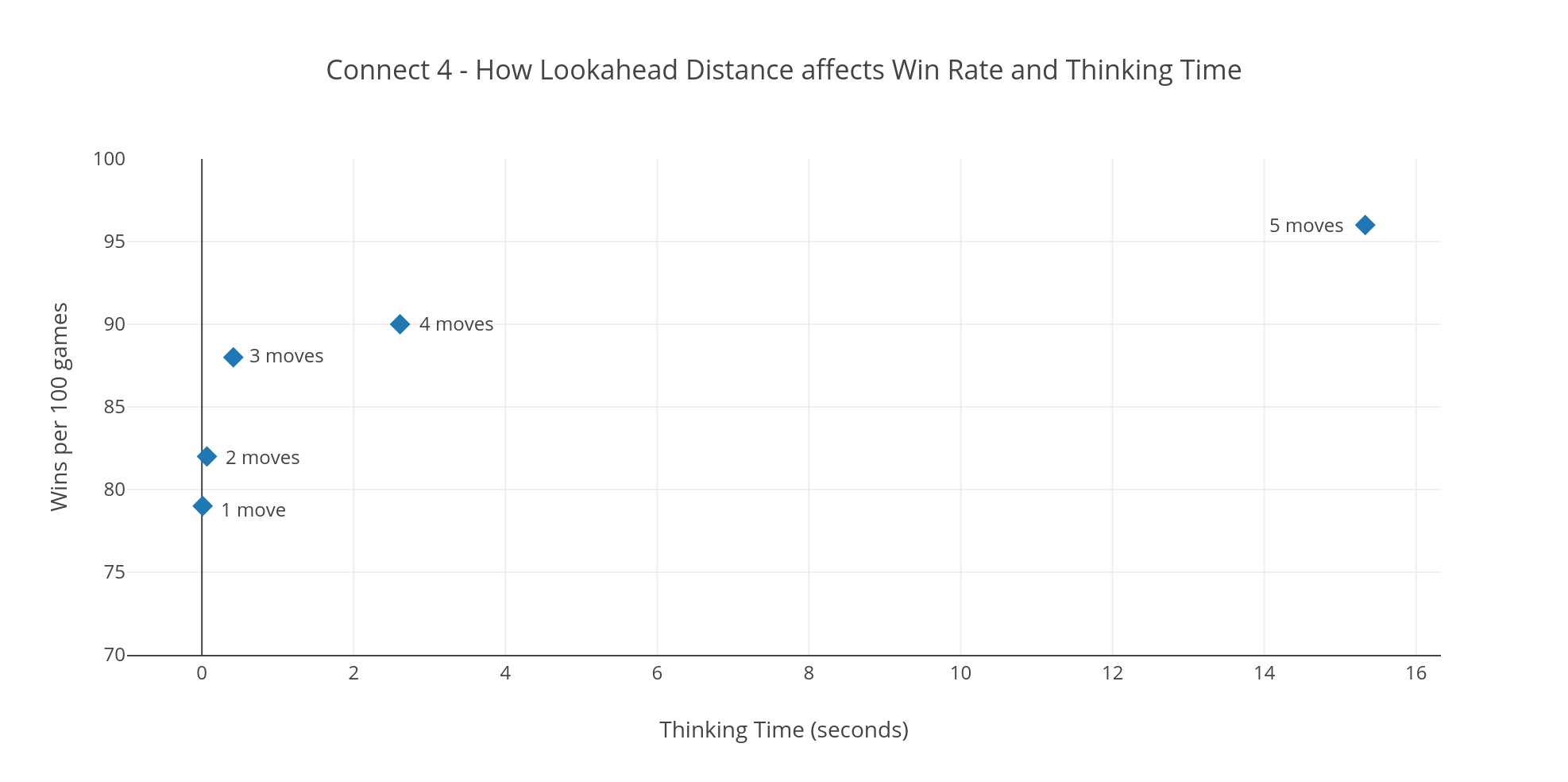
As expected, the addition of lookahead improved the strength of Connect Zero quite significantly, at the cost of some time performance. The diagram below shows how well different amounts of lookahead affected the win-rate against the MCTS-1000 player. For the final version of Connect Zero I chose 3-move lookahead, which gives a good win rate and sub-second thinking time.

Although I am quite pleased with how Connect Zero performs, there are many ways it could still be improved:

• Use Alpha-Beta Pruning when doing lookahead, this would allow the system to reduce thinking time and use more lookahead moves
• Train for longer, using a larger ensemble on a faster computer (all training for this project was done on my 5-year old MacBook Pro)
• Exploit the horizontal symmetry of Connect 4 by using mirror images of each board position to double the number of training examples shown to the Neural Network
• Experiment with the various hyper-parameters which I basically guessed at, such as Discounting Factor, Loss Function, Activation Function, Optimiser, Exploration Probability etc
• Try some more network architectures, perhaps using a second convolutional layer
• Add Drop Out to reduce over fitting - perhaps this will allow use of a single network rather than an ensemble, reducing training time